
Onthe 8th of May, 1945, Germany unconditionally surrendered to the Allies, bringing an end to the European theatre of World War II. Soon after, ten of Germany’s most prominent scientists involved in their nuclear weapons programme were captured and interned at a country estate in the United Kingdom called Farm Hall [1].
For the following six months, from the 3rd of July, 1945, to the 3rd of January, 1946 [2], they were each tasked with providing a detailed account of the development of German science throughout the war. However, unbeknownst to the captive nuclear scientists, each room in Farm Hall had been bugged with hidden microphones as part of an Allied intelligence programme codenamed Operation Epsilon [3]. One of the central objectives of which was to determine how close Nazi Germany had come to developing nuclear weapons.
Heisenberg’s Reaction to Hiroshima
It was in one such room that on the 6th of August, 1945, Werner Heisenberg, one of the founding fathers of Quantum Mechanics and lead scientists of Nazi Germany’s nuclear programme, and Otto Hahn, a German nuclear chemist credited for the co-discovery of nuclear fission (for which he won the Nobel prize in 1944), heard news crackle over the radio that Allied forces had dropped the first atomic bomb on Hiroshima.

As revealed in the now declassified transcripts, Heisenberg’s and Hahn’s initial reactions were those of absolute astonishment and disbelief. Immediately, Heisenberg declared the existence of an Allied atomic bomb impossible and disregarded the news of Hiroshima as a hoax, possibly created to hasten the end of the war with Japan or even to intimidate the Soviet Union, who were quickly becoming a competing global superpower to the West in the aftermath of the war. Heisenberg voiced his skepticism to Hahn [1]:
Heisenberg: “Some dilettante in America who knows very little about it has bluffed them. I don’t believe that it has anything to do with Uranium.”
This sparked fierce debate and technical discussion among the interned German scientists. However, as news came in over the radio just a few hours later of a second nuclear explosion over Nagasaki Heisenberg and the others were convinced of the bomb’s legitimacy.
The Critical Mass Problem
Central to their confusion was their belief in a wildly inaccurate estimation of how much uranium would actually be required to initiate an explosive nuclear fission chain reaction, i.e. to construct an atomic bomb. This mass of uranium is known as the critical mass and an accurate estimation of its value had proven to have profound and far-reaching consequences on the outcome of the war, as well as on the global balance of power in its aftermath.
In the transcript of a private conversation between Heisenberg and Hahn we can begin to get an insight into their understanding of the physics of nuclear fission bombs and how they approached the problem of calculating the critical mass. In their discussion Heisenberg described to Hahn his random walk (RW) model [4] of a nuclear fission chain reaction in a sphere of uranium and how it could be applied to estimate a critical mass of approximately 13 tonnes of enriched uranium [1].
Heisenberg estimated that a mass of 13,000 kg of enriched uranium would be needed to construct an atomic bomb.
The model that Heisenberg described to Hahn at Farm Hall and his huge overestimation of the critical mass closely match the content of a two-part technical report that Heisenberg presented to German Army Ordinance a few years earlier in 1939 and 1940 on the feasibility of constructing a nuclear fission bomb [5]. In these reports, Heisenberg concluded that an absolutely enormous industrial effort would be required to produce the tonnes of isotope-enriched uranium (using a process which at the time had just begun to be developed, never mind scaled to industrial levels) required to construct an atomic bomb.

As a result, Heisenberg and German Army Ordinance declared the atomic bomb project unfeasible and by 1942 it had been all but abandoned [4]. Instead, they directed their attention towards the peacetime application of harnessing abundant nuclear energy with nuclear reactors [1], comforted by their false belief that the Allies couldn’t possibly construct their own atomic bomb in the near future.
The Allied Approach to the Critical Mass Problem
However, as Allied nuclear scientists would figure out by 1940, and as Heisenberg himself would realise within days after the bombing of Nagasaki, a substantially smaller mass of uranium would suffice to construct an atomic bomb. Detailed in a 1940 memorandum to the British science advisor Henry Tizard, physicists Otto Frisch and Rudolf Peierls presented their neutron diffusion approach to the critical mass problem and demonstrated how it estimated a critical mass of just 600 grams of uranium! [1]
Allied physicists Frisch and Peierls estimated an atomic bomb could be constructed with just 600 grams of enriched uranium.
The Frisch-Peierls Memorandum quickly made its way to the United States and other Western Allies, immediately stimulating a rapid mobilisation of resources, engineers, and nuclear scientists towards the goal of developing nuclear weapons in an operation which would eventually become known as The Manhattan Project. The urgency of the project was spurred on by the belief that if they had figured out that a nuclear fission bomb was possible, then surely Nazi Germany’s own nuclear scientists would figure it out soon as well, if they hadn’t already.
Soon, a more elaborate recalculation, following the same basic principles laid out by Frisch and Peierls but using more up-to-date experimental parameters and more careful assumptions, by the American physicist Robert Serber showed that the critical mass of uranium was more realistically in the ballpark of 50 to 60 kg [1]. This was considerably larger than the initial estimation of 600 grams but by then it was considered a feasible amount of enriched uranium to produce.
By July 16, 1945, the first experimental atomic bomb had been constructed by the Allies and was detonated in the New Mexico desert in a test of the bomb’s explosive yield codenamed the “Trinity” test. Not long after, the atomic bomb which would eventually be dropped on Hiroshima was constructed, containing 64 kg of enriched uranium.
So how did Heisenberg and the other German nuclear scientists manage to get it so wrong? And how did Frisch, Peierls, and Serber correctly approach the problem such that they were able to accurately estimate the critical mass?
For the remainder of this article we’ll go into the mathematics and details behind Heisenberg’s random walk model and his back-of-the-envelope critical mass estimation.
Atomic Bomb Basics
Nuclear Fission
Nuclear fission refers to the process in which atoms of heavy elements, with large and unstable nuclei, are ‘split’ into two atoms of lighter elements, with smaller and more stable nuclei, after colliding with and absorbing a neutron. Each fission of a uranium nucleus releases vast amounts of stored nuclear energy, as well as more neutrons which can each go on to trigger more fission events.
However, not all elements are capable of undergoing nuclear fission, and even less are capable initiating and sustaining a nuclear fission chain reaction. Elements that can are referred to as being fissile. The uranium-238 isotope is an example of an element which is capable of undergoing fission but is not fissile. Meanwhile, the uranium-235 isotope is fissile.
Nuclear Fission Chain Reactions
Let’s now imagine that we have a very large sphere of pure uranium-235. In this case, a single fission event can set off a nuclear fission chain reaction in which the occurrence of fission events and the density of neutrons in the sphere explodes exponentially. This is in part because each fission event absorbs a single neutron and releases approximately two neutrons, which can each go on to trigger another fission event, creating a cascading effect.
Mean Free Path
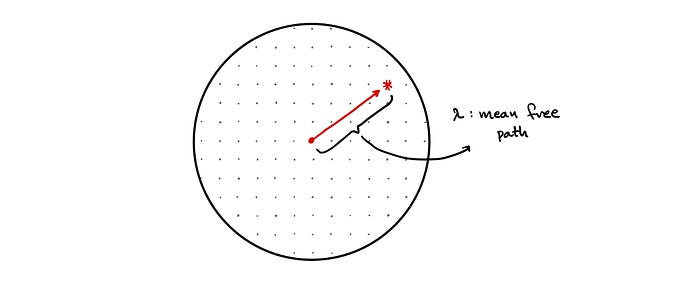
However, we have to remember that the nucleus of an atom is incredibly small relative to the total size of the atom. Thus, from the point of view of a neutron the sphere of uranium-235 is composed mostly of empty space. As a result, a neutron can travel great distances through the sphere of uranium before colliding with another nucleus.
This introduces us to a very important concept known as the mean free path. The mean free path 𝜆 describes the average distance that a neutron travels before it collides with another nucleus.
The Critical Mass and Radius
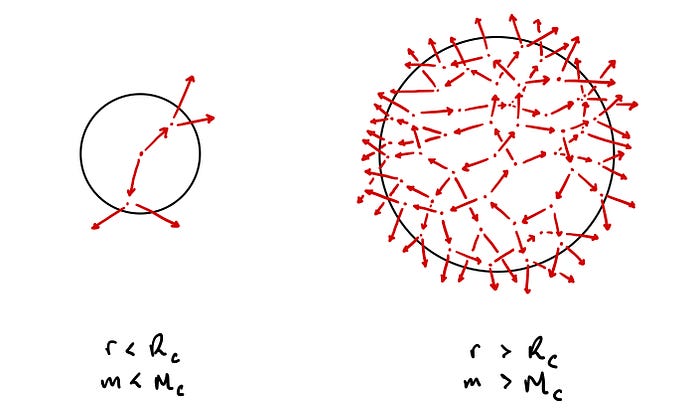
It becomes clear that if the radius of our sphere and its mass are too small then the average neutron produced within the sphere will travel through it and escape without ever colliding with another nucleus. Therefore, any nuclear fission chain reaction that begins will eventually fizzle out.
Conversely, if we have a massive sphere of pure uranium-235 then each neutron produced within the sphere effectively has a 100% probability of colliding with another nucleus before having the chance to escape. Thus we will have a sustained nuclear fission chain reaction, resulting in an exponential increase in the number of fission events and in the neutron density. In other words, we’ll have a nuclear explosion.
Therefore, there is some threshold mass, and corresponding threshold spherical radius, at which point the nuclear fission reaction transitions from fizzling out to taking off exponentially. These threshold values are known as the critical mass and the critical spherical radius of uranium.
Heisenberg’s Random Walk Approach
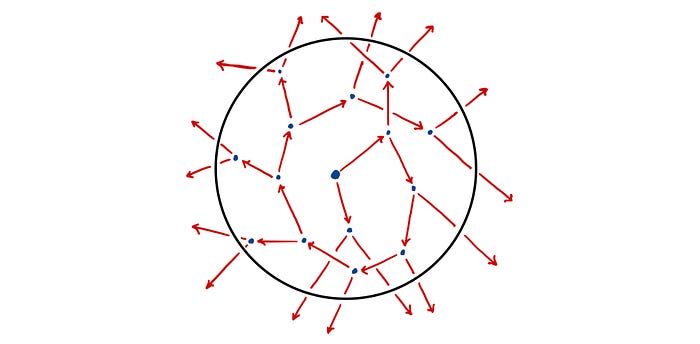
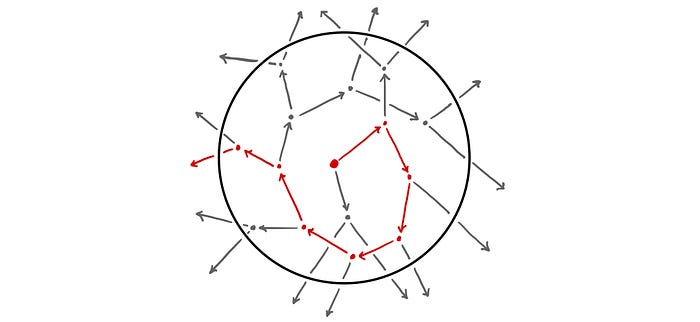
Heisenberg starts off by imagining a single neutron at the centre of a sphere of pure uranium-235. The neutron flies off in a random direction, travelling a mean free path length and colliding with a nucleus. This triggers a fission event and two neutrons are released, each of which flies off in a random direction travelling a mean free path length once again. This process repeats with each successive generation of neutrons exponentially increasing in number and gradually diffusing outwards from the centre of the sphere.
However, rather than thinking of a fission event as consisting of an absorption of a neutron and a production of two neutrons, Heisenberg instead re-imagines it as a scattering event in which the initial neutron is never absorbed but is instead scattered off the nucleus (releasing a second neutron in the process). As such, we can trace out the path of the initial neutron as it scatters from nucleus to nucleus as though in a pin-ball machine. This simple model of diffusion is known as a random walk [1]. A simple 2D example of a random walk is shown below.
For Heisenberg’s critical mass estimation he considered a three dimensional random walk in a sphere of uranium.
After some number of collisions, our initial neutron will reach the surface of the sphere and escape, having triggered some total number of fission events.
Based on this model, Heisenberg asked himself:
How large must the sphere be such that by the time the initial neutron has escaped, it has triggered a total number of N fission events?
As a goal post, Heisenberg chose the total number of fission events N to be 10²⁴ fissions. This corresponds to an energy release roughly equivalent to 15 kilotons of TNT [1].
Now, let n denote the number of collisions experienced by our initial neutron. We’ll use this parameter as a sort of iteration counter. We know that with each collision or iteration, the total number of neutrons doubles.
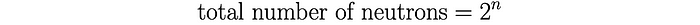
Each of these neutrons will then go on to trigger a fission event. Thus, Heisenberg uses the simple relation:
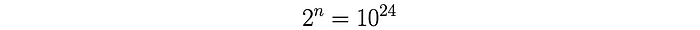
To calculate the number of collisions required to trigger 10²⁴ fission events:
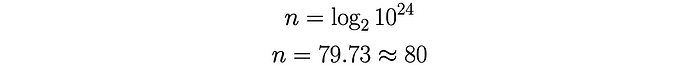
Therefore, Heisenberg determined that in order to have an explosive yield of 15 kilotons of TNT an initial neutron would need to experience roughly 80 collisions before escaping the sphere of uranium. So now the question becomes:
How large does the sphere need to be to ensure that the initial neutron experiences 80 collisions before it diffuses to the surface and escapes?
To figure this out let’s consider the simpler example of a one-dimensional random walk. We can imagine this as our neutron sitting on a 1D line. With each iteration (collision) our neutron randomly moves either one mean free path length to the right +𝜆 or to the left -𝜆.

Let’s say that that the neutron takes n random steps, each of which we will denote using aᵢ. For example, if the 3rd step is a step to the right then a₃ = +𝜆. We can therefore find the average of the distance squared according to the following:
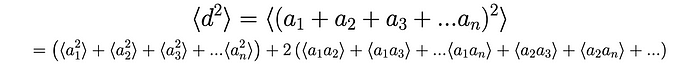
We know that each squared term, whether a = +𝜆 or a = -𝜆, is:
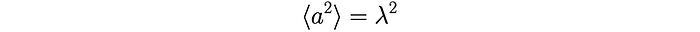
We also know that each product aₕaₖ has an equal probability of being +𝜆² (when h = k) or -𝜆² (when h ≠ k) and so their average is equal to zero. Therefore, the average of the distance squared becomes:
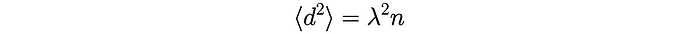
We finally arrive at the root-mean-squared distance:
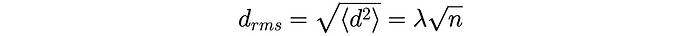
The same formula can also be applied to a random walk in 3D space. This is how Heisenberg relates the number of collisions n to the approximate distance travelled by the initial neutron from the centre of the sphere.
For his calculation, Heisenberg used a mean free path (calculated using experimentally measured parameters) of 𝜆 = 6 cm. Thus, to achieve 80 collisions Heisenberg estimated a critical radius of a sphere of uranium equal to:
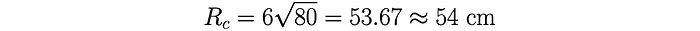
From here, the critical mass for a sphere of uranium can be easily calculated using the experimentally measured value for the density 𝝆 of uranium and the volume of a sphere. In Heisenberg’s time the most up-to-date value he had available for the density of uranium was 𝝆 = 19 g cm⁻³ (grams per cubic centimetre). Thus, Heisenberg estimated a critical mass of:
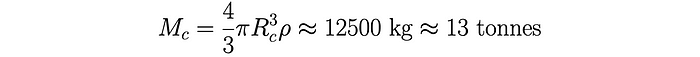
Where Heisenberg Went Wrong
Heisenberg’s random walk model might seem like a perfectly valid approach to the critical mass problem. However, hidden within it are a number of implicit assumptions which turn out to be either too strict or entirely false.
For starters, much of Heisenberg’s thinking on the problem was strongly influenced by the fundamental belief that the critical radius of a sphere of uranium ought to be larger than the mean free path of uranium [1]. Initially, this belief might seem intuitive and perfectly legitimate. If the mean free path describes the distance that a neutron travels before colliding with a uranium nucleus then it naturally follows that if we have a sphere with a radius smaller than the mean free path then neutrons produced within it will be able to travel to the surface and escape without any collisions with uranium nuclei. However, as the Allied physicists Frisch and Peierls show, it turns out that the critical radius of uranium is smaller than its mean free path.
Frisch and Peierls showed somewhat counter-intuitively that the critical radius is smaller than the mean free path.
There are two factors that Heisenberg’s belief did not consider. Firstly, we need to recall that the mean free path is an average [1]. If we have many neutrons flying off in random directions from the centre of our sphere then a great number of them will collide with a uranium nucleus before travelling a mean free path to the surface and escaping.
Although the average neutron does escape the sphere, if enough do not escape then it becomes possible to sustain a nuclear fission chain reaction.
Secondly, only neutrons originating from the centre of the sphere were considered. In reality, most neutrons will have been produced elsewhere in the sphere, some even close to the surface, and they won’t necessarily be travelling outwards from the centre of the sphere. In the most extreme case, there might be a neutron produced very close to the surface which is travelling inward towards the centre of the sphere. This neutron would thus have two mean free paths ahead of it in which it could collide with a uranium nucleus. Although this is clearly a rare case, one could imagine that a not-so-insignificant proportion of neutrons generated within the sphere have at least a mean free path or more ahead of them in their direction of travel through the uranium sphere.
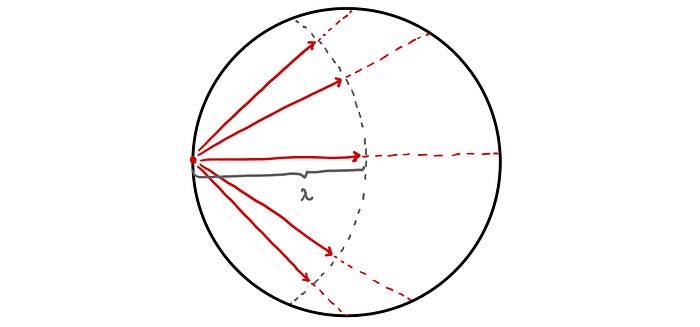
Finally, Heisenberg’s random walk approach assumes that each neutron generated needs to initiate some number of fission events, in his calculation he used 10²⁴, before escaping the sphere [4]. This simply turns out to be too strict and too simple a condition [1] which fails to capture the exponential nature of a nuclear fission chain reaction.

